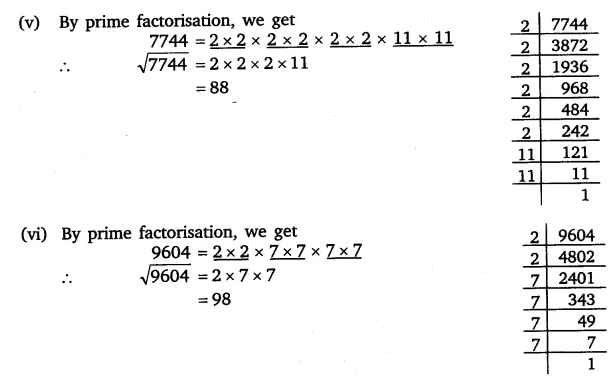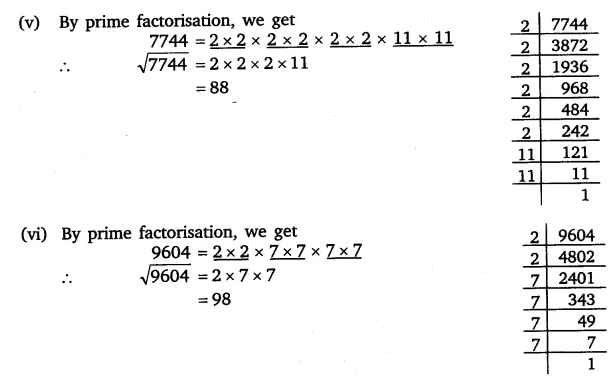Find The Square Root Of 484 By Prime Factorization Method

Find the product of factors obtained in step iv.

Find the square root of 484 by prime factorization method.

Square root of 484. Use the prime factorization method to decide if these numbers are perfect squares and to find the square roots of those that are perfect squares. This is a step by step guide for finding the value of square root of 4096 for finding the square root of any number we have two methods. Ii inside the square root for every two same numbers multiplied one number can be taken out of the square root.

For example 4 has two square roots. We conclude that 84 is not a perfect square and does not have a square root that is a whole number. The square root radical is simplified or in its simplest form only when the radicand has no square factors left. Generally prime factorization is used for finding square roots of small numbers.

The product obtained in step v is the required square root. We can find square root by prime factorization method or by long division method. To find the square root of a perfect square by using the prime factorization method when a given number is a perfect square. The peculiarity of the four is that both 2 2 4 and 2 2 4 and thus 2 2 4.

Four points make the plane of a square an area with four sides. Thew following steps will be useful to find square root of a number by prime factorization. A whole number with a square root that is also a whole number is called a perfect square. In this video we have studied how to find squares of a given number by using prime factorization method.

0 00 how to fin. Is 484 an odd number. Take the product of prime factors choosing one factor out of every pair. It is the first composite number and thus the first non prime number after one.

To learn more about squares and square roots enrol in our full course now. Since there is an even number of prime factors and they can be grouped in identical pairs. Since the number is a perfect square you will be able to make an exact number of pairs of prime factors. Make pairs of similar factors.

Square root by prime factorization method example 1 find the square root. Take one factor from each pair. I decompose the number inside the square root into prime factors. Resolve the given number into prime factors.

The only square root of zero is zero.